

Lecture plans:
This set of two lectures covered the probabilistic aspect of analysis on fractals, complementing the tutorials by Bob Strichartz.
It covers the essential ideas needed to read, for instance, Martin Barlow's St. Flour lecture notes "Diffusions on fractals",
and Takashi Kumagai's St. Flour lecture notes "Random walks on disordered media and their scaling limits".
Using the language of Markov chains, I explained the significance of harmonic functions, Green's functions, and heat kernels in the study of
diffusions on fractals. I will also touched on various types of stopping times in Markov processes (hitting times, commute times, etc.) and their
connections to electric network theory.
Lecture 1 (06/15/2017): Covered the basics of Markov chains, focusing on symmetric random walks on unweighted graphs. Using one-step calculations we connected hitting probabilities to harmonic functions, and expected hitting times to Laplacian-1 functions (integrals of Green's functions). Motivating example: gambler's ruin (in 1D).
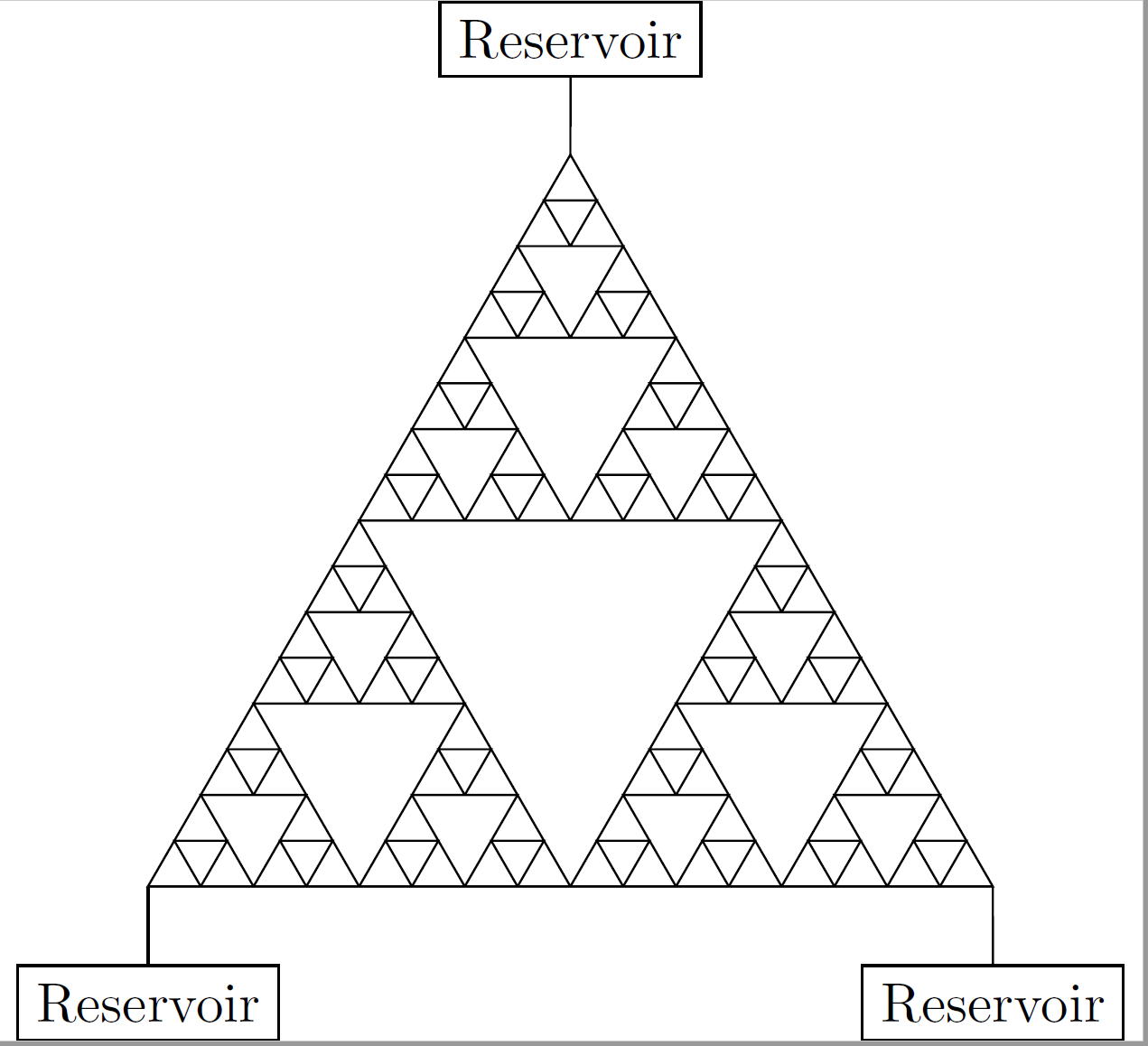
Lecture 2 (06/16/2017): Generalization to symmetric random walks on weighted graphs. Green's functions and heat kernels. Explicit calculations on SG (showing the time scale factor 5). Connections to effective resistance: escape probability, commute-time identity.
Besides the tutorial, I gave a 30-minute talk (on June 14) entitled "Strong shape theorems in cellular automata models on the Sierpinski gasket," covering recent results obtained with my Colgate undergraduate mentee Jonah Kudler-Flam. PDF Talk slides


Dates:
Mi. 12.07, Fr. 14.07, Mo. 17.07, Mi. 19.07, Fr. 21.07.
Times: Mo. & Mi. 12:15~14:00; Fr. 10:15~12:00.
Room: D5-153.
Actual lecture outline:
Synopsis:
I will start by discussing the basics of particle systems on graphs and their connections to
the random walk process and the relevant potential theory. Emphasis will be on results and techniques which are applicable to non-transitive graphs.
After the introductory lecture(s), I will describe two classes of particle systems for which the scaling limits are mostly known on Euclidean lattices,
but whose generalizations to fractal lattices have only been established recently.
For concreteness, I will use the Sierpinski gasket as the model graph, and describe the limit theorems for the aforementioned processes. Though I will say a few words about (variants of) these models on other fractal (or general weighted) graphs, and mention connections to aspects of non-equilibrium statistical mechanics.
This course assumes working knowledge of real analysis and probability theory at the advanced undergraduate / intro graduate level. Exposure to Markov chains is useful but not necessary.
References:
Introductory materials are drawn from a variety of sources.
Acknowledgements. I am grateful to Prof. Dr. Moritz Kassmann and Dr. Michael Hinz for arranging this opportunity.