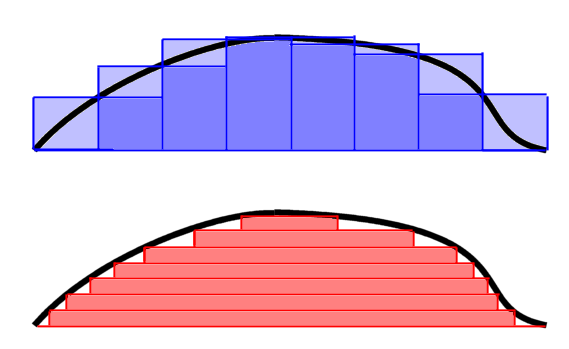
Images courtesy of Wikipedia: Riemann vs. Lebesgue integration (left); a Fourier series (middle); and blowups of a 1D Brownian motion trajectory (right)
MATH 487 - Real Analysis II (Spring 2020): Measure Theory, Fourier Analysis, and Brownian Motion
UNDER CONSTRUCTION
Instructor: Joe P. Chen
Contact: McGregory 214, jpchen-at-(the obvious edu)
Course philosophy:
This is a second-semester course on mathematical analysis, covering two topics which are mutually connected:
- Convergence of (series of) functions.
- A more robust theory of integration called Lebesgue integration.
In treating these topics together, we will simultaneously learn about function spaces, in particular, the space of continuous functions, and \(L^p\) spaces (\(p\in [1,\infty]\)).
\(L^2\) spaces are important in their own right---they are Hilbert spaces---and allow us to characterize properties of Fourier series.
An additional motivation for this course comes from probability (coin tosses and random walks) and partial differential equations (Laplace’s equation, and its discrete analog, the gambler’s ruin problem; and the heat equation).
Towards the end of the course, we will use what we learned to construct the space-time scaling limit of random walks, called Brownian motion---it can be realized as a random Fourier series!
Prerequisites:
Strong performance in Real Analysis I (MATH 377). Some exposure to complex variables and/or basic probability is helpful, but not required.
Back to the Colgate math department